Radicals and Rational Exponents
Introduction
Radicals are really about dividing exponents. In this section, we’ll see how
that idea leads us to fractional
exponents, and how all of the usual rules for exponents apply even when the
exponents are fractions. This
concept gets to the heart of radicals and is the key to solving many problems
involving radicals. In fact,
you need to know how radicals are equivalent to fractional exponents in order to
evaluate radicals (other
than square roots) on a typical scientific calculator.
Although you already know that the square root of nine is three, focus
carefully on the new way of
looking at this simple square root problem illustrated in the following example.
How does taking the square root of nine involve dividing exponents? It turns
out to be a matter of “two
goes into two once with no remainder”:
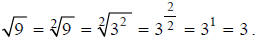
Not only is the radical symbol
 similar to the long division symbol
similar to the long division symbol
 ,
it really does indicate
,
it really does indicate
division—division of exponents.
Example A involves a fifth-root radical expression, and it has a remainder.
Example A
Simplify:
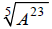
We’ll come back to this example a little later, to look at each step in
depth. For now, just watch
how the overall process unfolds…
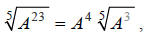
“5 goes into 23, 4 times with a remainder of 3”.
Notice that the remainder actually does remain under the radical.
Considering this example, it makes sense to write:
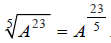
More generally, an nth root divides exponents by n , so we can write:
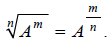
That last equation is a bridge between radicals and
exponents. Crossing this bridge gives us
access to the powerful exponent properties that you know (and love) so well…but
if you don’t
know them quite so well, this may be a good time to review the Properties of
Exponents (see the
table on the next page).
Chapter 6 Section 2 Lesson: Radicals and Rational
Exponents
Properties of Exponents
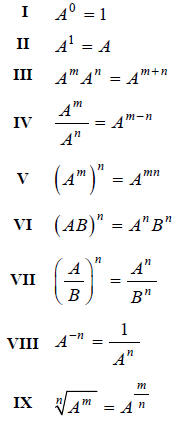
Now let's redo Example A, but just using exponents.
Example B
Simplify:
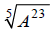
Above, we learned that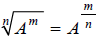 It
can help to see how this is true by noting that
It
can help to see how this is true by noting that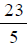 as a
as a
mixed number is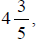 which means
which means
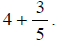
See how this relates to the process below (each exponent
rule used is referred to by its Roman
numeral in the Properties of Exponents table):
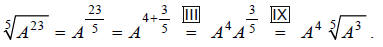
Using a Calculator to Find Roots
How do we find a numerical approximation to expressions
like 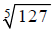 using a standard scientific
using a standard scientific
calculator? Calculators have square root buttons but no fifth root buttons, so
what do we do? Fractional
exponents, to the rescue!
Chapter 6 Section 2 Lesson: Radicals and Rational
Exponents
Example C
Evaluate:
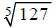
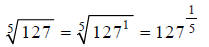
The word “evaluate” here implies that we want a numerical
approximation to this radical. So, go
get your calculator.
Scientific calculators allow you to raise numbers to
powers. Try to compute this on your
calculator. On some calculators you enter:
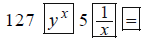
On others, including the one mentioned in the Introduction
to this section, enter:
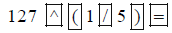
If you have a “reverse-Polish” calculator, enter:
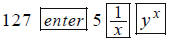
Note: Some calculators have an
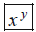 button not
button not
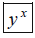 . They do the same thing.
. They do the same thing.
You should get something close to
2.634879412770604848540719 (though probably with
fewer digits).
It’s very important that you know how to compute radicals
on your calculator. Consult your
calculator’s manual if none of the methods above work for you.
Extended Example 1a
Approximate 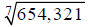 to the nearest millionth.
to the nearest millionth.
Hint: Rewrite, using fractional exponents.
Step 1:
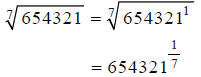
Hint: Compute this on your calculator.
Step 2:
 6.77372038951128 (Your result may vary,
slightly!)
6.77372038951128 (Your result may vary,
slightly!)
Hint: Round your result to the nearest millionth.
Answer:
 6.77372038951128
6.77372038951128
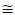 6.773720
6.773720
Chapter 6 Section 2 Lesson: Radicals and Rational
Exponents
Extended Example 1b
Approximate 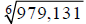 to the nearest millionth.
to the nearest millionth.
Hint: Rewrite, using fractional exponents.
Step 1:
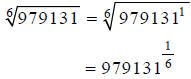
Hint: Compute this on your calculator.
Step 2:
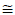 9.96491197718962 (Your result may vary,
slightly!)
9.96491197718962 (Your result may vary,
slightly!)
Hint: Round your result to the nearest millionth.
Answer:
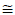 9.96491197718962
9.96491197718962
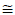 9.964912
9.964912
Extended Example 1c
Approximate  to the
nearest millionth.
to the
nearest millionth.
Hint: Rewrite, using fractional exponents.
Step 1:
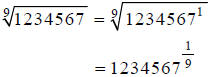
Hint: Compute this on your calculator.
Step 2:
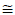 4.75154626941184 (Your result may vary,
slightly!)
4.75154626941184 (Your result may vary,
slightly!)
Hint: Round your result to the nearest millionth.
Answer:
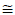 4.75154626941184
4.75154626941184
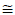 4.751546
4.751546
Example D
Approximate  to the
nearest millionth.
to the
nearest millionth.
First we rewrite the radical, using fractional exponents:
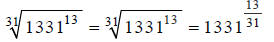
Notice how the root (the index) becomes the denominator,
and the exponent under the radical
becomes the numerator.
Computing this on my calculator, I get:
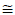 20.4239239445 (Your result may vary,
slightly!)
20.4239239445 (Your result may vary,
slightly!)
Rounding to the nearest millionth, I obtain:
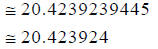
Chapter 6 Section 2 Lesson: Radicals and Rational
Exponents
Extended Example 2a
Approximate  to the nearest
hundred-thousandth.
to the nearest
hundred-thousandth.
Hint: Rewrite, using fractional exponents.
Step 1:
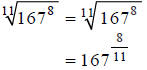
Hint: Compute this on your calculator.
Step 2:
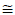 41.3543377040440 (Your result may vary,
slightly!)
41.3543377040440 (Your result may vary,
slightly!)
Hint: Round your result to the nearest hundred-thousandth.
Answer:
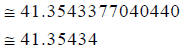
Extended Example 2b
Approximate  to the nearest
hundred-thousandth.
to the nearest
hundred-thousandth.
Hint: Rewrite, using fractional exponents.
Step 1:
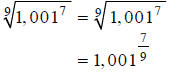
Hint: Compute this on your calculator.
Step 2:
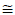 215.611017534756 (Your result may vary,
slightly!)
215.611017534756 (Your result may vary,
slightly!)
Hint: Round your result to the nearest hundred-thousandth.
Answer:
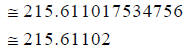
Extended Example 2c
Approximate 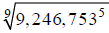 to the nearest
hundred-thousandth.
to the nearest
hundred-thousandth.
Hint: Rewrite, using fractional exponents.
Step 1:
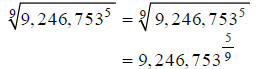
Hint: Compute this on your calculator.
Step 2:
 7413.00053725752 (Your result may vary,
slightly!)
7413.00053725752 (Your result may vary,
slightly!)
Hint: Round your result to the nearest hundred-thousandth.
Answer:
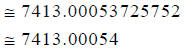
Chapter 6 Section 2 Lesson: Radicals and Rational
Exponents
Next we'll see how algebraic properties of radicals can be
understood in terms of the familiar properties of
exponents. But first, study the following properties of radicals.
Example 1
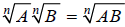 , n odd. Examples:
, n odd. Examples:
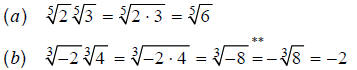
**This step is true because (using this rule in reverse):
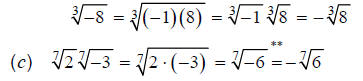
**This step is true because (using this rule in reverse):
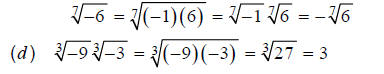
Chapter 6 Section 2 Lesson: Radicals and Rational
Exponents
continued…
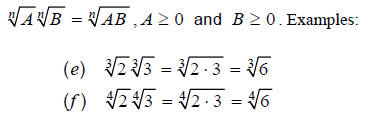
Example 2
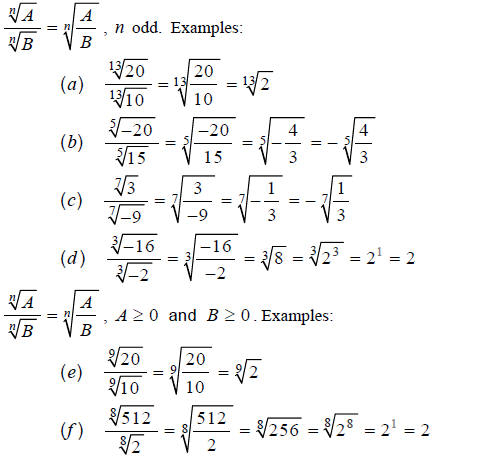
As usual, we must always have nonzero denominators, since
division by zero is undefined.
Example 3
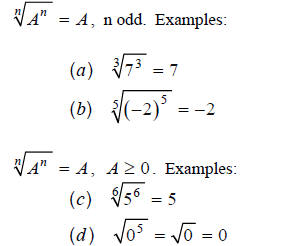
Chapter 6 Section 2 Lesson: Radicals and Rational
Exponents
continued…
Example 4
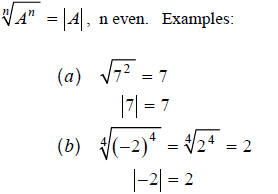
Example 5
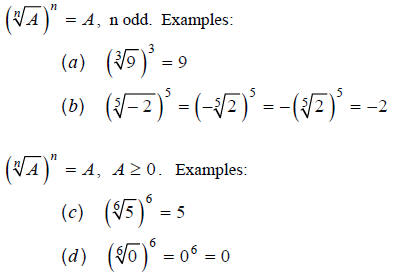
Example E
Approximate 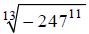 to the
nearest millionth.
to the
nearest millionth.
For odd roots, a negative under the radical can come out
of the radical, as we saw in the previous
section:
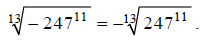
Note that this is possible because (using the
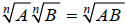 property of radicals shown in the
property of radicals shown in the
table above):
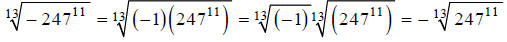
Next we rewrite the radical, using fractional exponents:
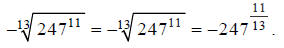
Chapter 6 Section 2 Lesson: Radicals and Rational
Exponents
Example E, continued…
Notice how the index becomes the denominator, and the
exponent of the radicand becomes the
numerator.
Calculate 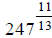 on your
calculator, and don’t forget to keep the negative in front of your final
on your
calculator, and don’t forget to keep the negative in front of your final
answer:
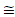 −105.825353941 (Your result may vary,
slightly.)
−105.825353941 (Your result may vary,
slightly.)
Rounding off to the nearest millionth, we get:
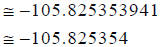
Now we'll see how the properties of radicals arise from
the properties of exponents.
Example F
Translate the leftmost and rightmost of the sequence of equalities below into
radical notation:
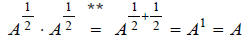
**Note: This is a valid step, due to the following
property of exponents:
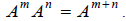
Since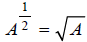 , (because
, (because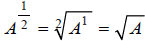 ),
we have an important property of exponents:
),
we have an important property of exponents:
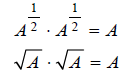
This leads us to this property of radicals:
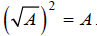
Recall that this is true only when A is non-negative. So,
to be well-defined, only non-negative
numbers may be raised to rational powers with an even denominator (reduced to
lowest terms).
Important Note
In this course you can assume the appropriate
conditions are met when doing algebra with
exponents. From now on, you can assume that all
variables represent positive quantities unless it is
clearly stated that they do not.
Chapter 6 Section 2 Lesson: Radicals and Rational
Exponents
Example G
Translate the leftmost and rightmost of the sequence of equalities below into
radical notation:
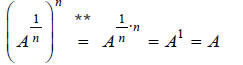
**Note: This is a valid step, due to the following
property of exponents:
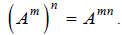
Substituting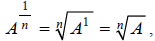 we get
we get
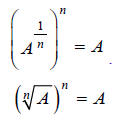
This result, 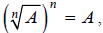 , is
radical property V in the Properties of Radicals table. Recall that the
, is
radical property V in the Properties of Radicals table. Recall that the
result of Example F was the property 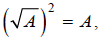 which
is also property V, but with n = 2 :
which
is also property V, but with n = 2 :
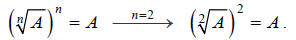
(Don’t forget that an index of 2 is always implied for
square roots: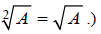
Example H
Translate the following equation into radical notation:
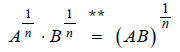
**Note: This is a valid step, due to the following
property of exponents:
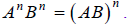
Substituting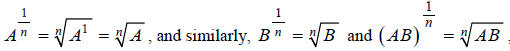 we get:
we get:
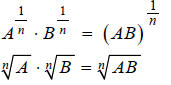
This is radical property I in the Properties of Radicals
table.
Chapter 6 Section 2 Lesson: Radicals and Rational
Exponents
Graphing Radical Functions using Fractional Exponents
Now we’ll see how to graph functions by using fractional exponents to calculate
the points to plot.
Example I
Graph the function 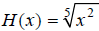 over the interval [−6,6]
.
over the interval [−6,6]
.
To graph H , first rewrite it using fractional exponents:
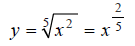
Next we make a table of x, y values that satisfy the
equation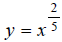 (using a calculator). In the
(using a calculator). In the
table, all values are rounded to the nearest hundredth:
Then we plot the points found:
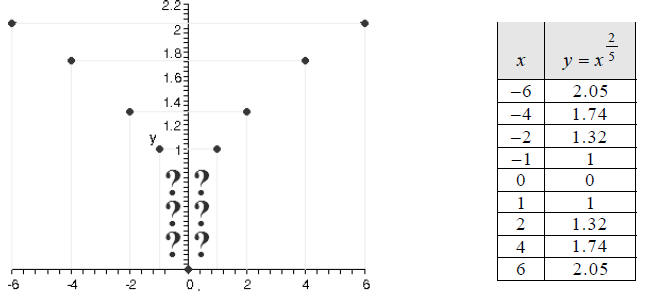
Be on the lookout for “regions of uncertainty,” where you
need to plot additional points. This
happens whenever the change in a graph is abrupt, and you aren’t sure where the
graph should go,
as in the region indicated by question marks in the graph above.
We’ll plot two more points, at x = −0.25 and x = 0.25 , to
better see how the curve passes
through the region of uncertainty.
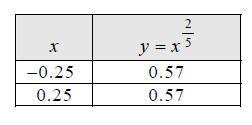
Chapter 6 Section 2 Lesson: Radicals and Rational
Exponents
Example I, continued…
Adding these two points to our plot, we can then connect
the dots:
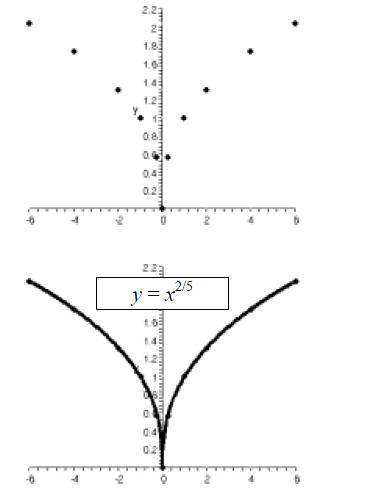
Points like (0,0) in the graph above are called cusps.
Note: There is an animation of this example in the course online
Example J
Graph the function 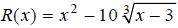 over the interval [0,6].
over the interval [0,6].
First, rewrite the function using fractional exponents.
Make a table of x, y values that satisfy the equation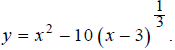
Use x -values 0,1, 2,3, 4,5,6 and round to the nearest
hundredth.
Chapter 6 Section 2 Lesson: Radicals and Rational
Exponents
Example J, continued…
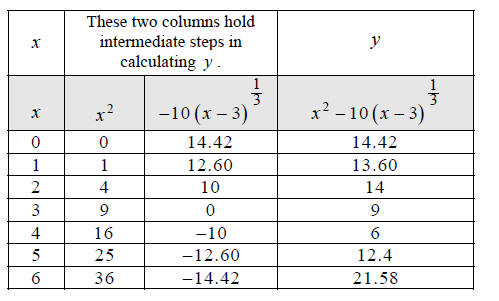
Plot the seven points we found
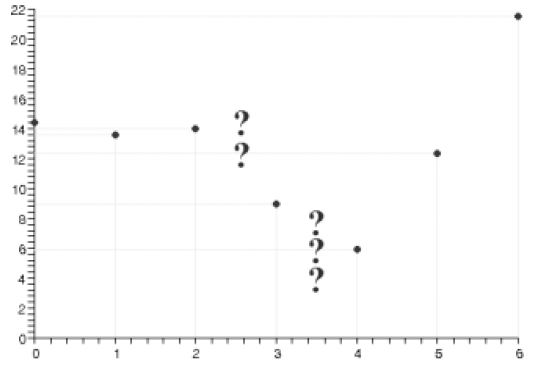
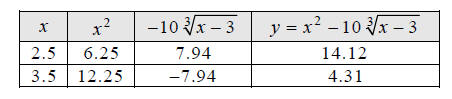
Find and plot two more points, say at x = 2.5 and 3.5, to
better see where the curve passes
through the regions of uncertainty (indicated with question marks).
Chapter 6 Section 2 Lesson: Radicals and Rational
Exponents
Example J, continued…
Plot the two additional points.
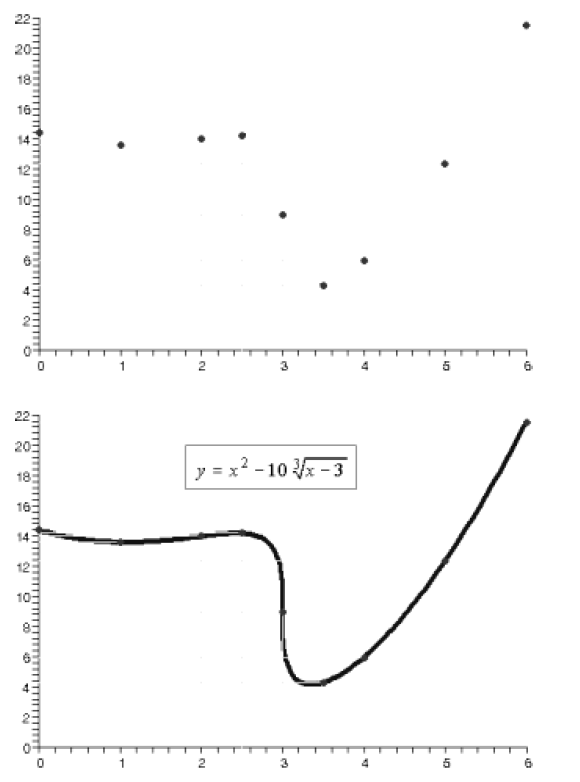
Note: The graph shown is a precise graph of the function,
done by a computer program. To approach this
accuracy by hand, it would be necessary to plot at least two additional points,
say at x = 2.75 and at
x = 3.25 .
Chapter 6 Section 2 Lesson: Radicals and Rational
Exponents
Extended Example 3a
Graph the function 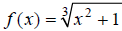 over the interval [−2, 2]
.
over the interval [−2, 2]
.
Hint: Rewrite the equation
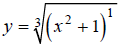 , using fractional exponents.
, using fractional exponents.
Step 1:
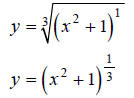
Hint: Make a table of x, y values that satisfy the
equation 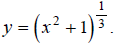 Use x -values
Use x -values
−2, − 1, 0,1, 2 and round to the nearest hundredth.
Step 2:
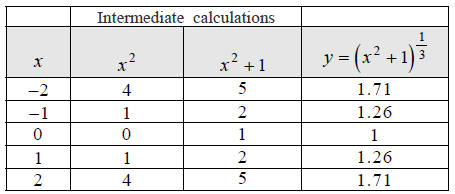
Hint: Plot these five points you just found.
Step 3:
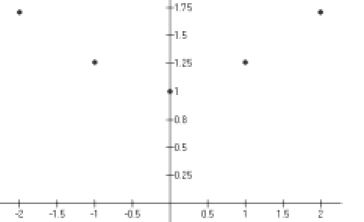
Hint: Smoothly connect the dots.
Answer:
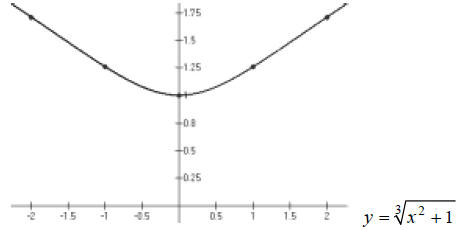
Chapter 6 Section 2 Lesson: Radicals and Rational
Exponents
Extended Example 3b
Graph the function 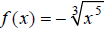 over the interval [−2, 2]
.
over the interval [−2, 2]
.
Hint: Rewrite the equation 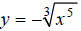 , using fractional
exponents.
, using fractional
exponents.
Step 1:
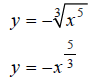
Hint: Make a table of x, y values that satisfy the
equation 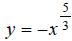 . Use x -values
. Use x -values
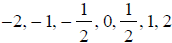 and round to the nearest hundredth.
and round to the nearest hundredth.
Step 2:
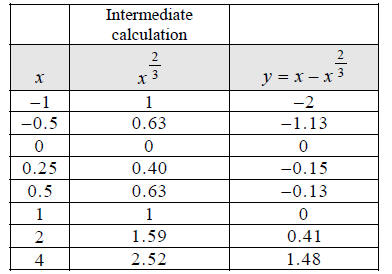
Intermediate
calculation
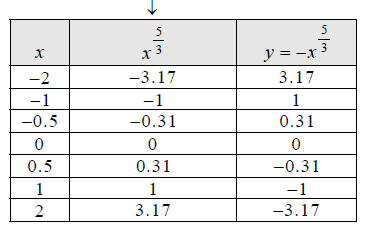
Hint: Plot these eight points you just found.
Step 3:
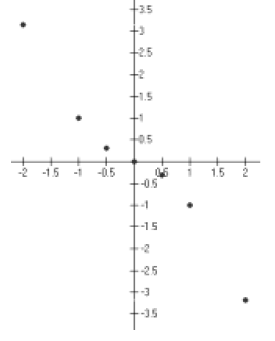
Hint: Smoothly connect the dots.
Chapter 6 Section 2 Lesson: Radicals and Rational
Exponents
Extended Example 3b, continued…
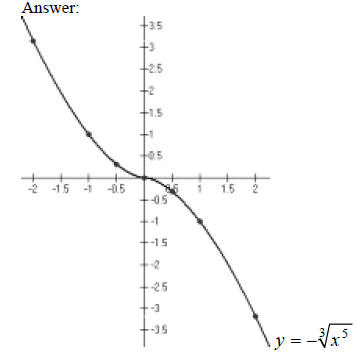
Extended Example 3c
Graph the function 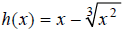 over the interval [−1, 5]
.
over the interval [−1, 5]
.
Hint: Rewrite the equation 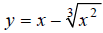 , using fractional
exponents.
, using fractional
exponents.
Step 1:
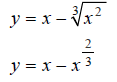
Hint: Make a table of x, y values that satisfy the
equation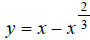 . Use x -values
. Use x -values
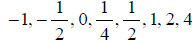 and round to the nearest hundredth.
and round to the nearest hundredth.
Step 2:
Chapter 6 Section 2 Lesson: Radicals and Rational
Exponents
Extended Example 3c, continued…
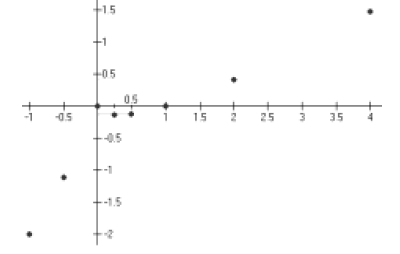
Hint: Plot these eight points you just found.
Step 3:
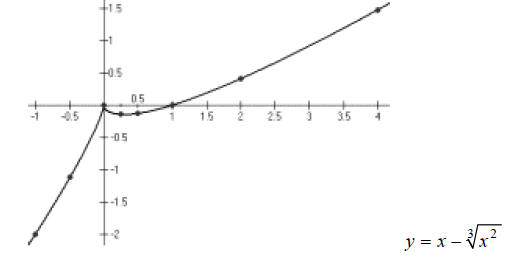
Hint: Smoothly connect the dots.
Answer:
End of Lesson